Hyperloglog Algorithm: A must-know for data scientists

Being able to act on insights from mobile data in real time is key to mobile data management. Before we think about fancy things like building a data pipeline that delivers predictive insights in real time, we need to focus on some basic but critical statistics of your mobile apps. In this blog post, I will review a powerful streaming algorithm, Hyperloglog (HLL), and discuss how it helps mParticle deliver low latency and high throughput analytics products.

The problem

mParticle platform provides real time activity reports of your mobile apps, e.g., how much data is captured and how much data is forwarded to service providers of your choice. We update KPI’s of your apps within seconds of data arriving at our servers so that you always get a hold of what’s going on. One of the key metrics is unique users during a time period. Pre-calculating unique user counts is not an option since there are too many scenarios to calculate and, more importantly, developers are always interested in knowing the number of active users on their apps right now.

Hyperloglog to the rescue

Hyperloglog is a space-efficient algorithm for accurate cardinality estimations. Nowadays a lot of data products use it, including Redis, AWS Redshift, and Druid. Redis’s implementation of HLL uses at most 12Kb of memory to estimate the cardinality of practically any set. HLL is such a “magical” algorithm that ever since I learned it, I always want to kick myself for not knowing it earlier.

The basic idea of HLL is as follows. Imagine you flip a coin for 100 times and count the number of consecutive heads before the first tail. Let’s call this one experiment. You perform a few experiments, and you may get the following series (H for head and T for tail):

experiment 1: HHTHTTHH….

experiment 2: HTHHHTTT….

experiment 3: TTHTHHHT….

The number of consecutive heads at the beginning of the series is 2, 1, 0, respectively, marked in red. If you only do a small number of experiments, the chance is that the max number of consecutive heads is small. However, if you have patience to perform a lot of experiments, you may get a large number of consecutive heads from at least one experiment.

If you are a fan of Bitcoin mining, you may find this somewhat familiar. Essentially, Bitcoin mining increases its difficulty by increasing the required number of consecutive leading 0’s in hashes, which means that you have to try a larger number of times to get lucky.

HLL essentially hashes every element in a set, counts the number of consecutive leading 0’s from each hash, and estimates the cardinality based on the largest count of consecutive leading 0’s out of the hashes.

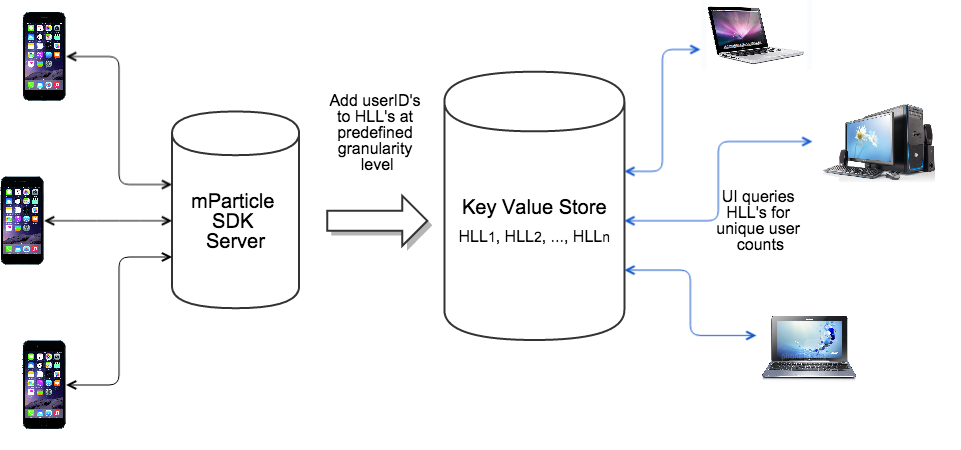
The graph below shows how HLL fits into our backend systems. We keep HLL keys for predefined data granularity levels, and query them for cardinality estimations whenever ad-hoc requests from UI come in. For example, we use one HLL data structure to store user ID’s per app per day. When a request comes in for unique user count in app XYZ between Oct 1, 2014 and Oct 21, 2014, we simply combine 21 daily HLL’s for app XYZ and estimate the unique user count.

More than just cardinality

HLL can be used for more than estimating cardinality of a given set. Two particularly interesting use cases for us are

1. Estimate the cardinality of union of multiple sets. It is natural to combine multiple HLL’s; simply take the largest count of consecutive leading 0’s from all the HLL’s.
2. Estimate the overlap of two sets. Since |A ∩ B| = |A| + |B| – |A ∪ B|, the overlap of two sets can be calculated from the cardinality of each set and the cardinality of their union.

Final words

Hyperloglog really deserves a spot in every data scientist’s toolbox and should be a cornerstone for “big data” systems. It only takes me 100-ish lines of python code to implement HLL for cardinality estimation, including support for set unions and overlap estimation. Can’t be easier than that!

Hope you are a fan of HLL by now. Here’s a list of useful links if you want to learn more.

• Original HLL paper by Philippe Flajolet.
• Google’s research on HLL, which further reduces memory requirements and increases accuracy on small cardinalities.
• A series of very useful blogs by Aggregate Knowledge (acquired by Neustar).

There are a few other use cases of streaming algorithms at mParticle, e.g., use Count-Min sketch to estimate quantiles, which I will talk about in a future post.